- Research
- Open access
- Published:
Stochastic Oscillations in Genetic Regulatory Networks: Application to Microarray Experiments
EURASIP Journal on Bioinformatics and Systems Biology volume 2006, Article number: 59526 (2006)
Abstract
We analyze the stochastic dynamics of genetic regulatory networks using a system of nonlinear differential equations. The system of  -functions is applied to capture the role of RNA polymerase in the transcription-translation mechanism. Using probabilistic properties of chemical rate equations, we derive a system of stochastic differential equations which are analytically tractable despite the high dimension of the regulatory network. Using stationary solutions of these equations, we explain the apparently paradoxical results of some recent time-course microarray experiments where mRNA transcription levels are found to only weakly correlate with the corresponding transcription rates. Combining analytical and simulation approaches, we determine the set of relationships between the size of the regulatory network, its structural complexity, chemical variability, and spectrum of oscillations. In particular, we show that temporal variability of chemical constituents may decrease while complexity of the network is increasing. This finding provides an insight into the nature of "functional determinism" of such an inherently stochastic system as genetic regulatory network.
-functions is applied to capture the role of RNA polymerase in the transcription-translation mechanism. Using probabilistic properties of chemical rate equations, we derive a system of stochastic differential equations which are analytically tractable despite the high dimension of the regulatory network. Using stationary solutions of these equations, we explain the apparently paradoxical results of some recent time-course microarray experiments where mRNA transcription levels are found to only weakly correlate with the corresponding transcription rates. Combining analytical and simulation approaches, we determine the set of relationships between the size of the regulatory network, its structural complexity, chemical variability, and spectrum of oscillations. In particular, we show that temporal variability of chemical constituents may decrease while complexity of the network is increasing. This finding provides an insight into the nature of "functional determinism" of such an inherently stochastic system as genetic regulatory network.
[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38]
References
Bower JM, Bolouri H (Eds): Computational Modeling of Genetic and Biochemical Networks. MIT Press, Cambridge, Mass, USA; 2001.
Boxler P: A stochastic version of center manifold theory. Probability Theory and Related Fields 1989,83(4):509-545. 10.1007/BF01845701
Bradley R: Basic properties of strong mixing conditions. A survey and some open questions. Probability Surveys 2005, 2: 107-144.
Bressan A: Tutorial on the Center Manifold Theory. 2003.http://www.math.psu.edu/bressan/PSPDF SISSA, Trieste, Italy,
Cai L, Friedman N, Xie XS: Stochastic protein expression in individual cells at the single molecule level. Nature 2006,440(7082):358-362. 10.1038/nature04599
Carr J: Applications of Center Manifold Theory. Springer, New York, NY, USA; 1981.
Chen F: Introduction to Plasma Physics and Controlled Fusion. Plenum Press, New York, NY, USA; 1984.
Chen T, He HL, Church GM: Modeling gene expression with differential equations. Pacific Symposium on Biocomputing (PSB '99), Mauna Lani, Hawaii, USA, January 1999 29-40.
De Jong H: Modeling and simulation of genetic regulatory systems: a literature review. Journal of Computational Biology 2002,9(1):67-103. 10.1089/10665270252833208
Elf J, Ehrenberg M: Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Research 2003,13(11):2475-2484. 10.1101/gr.1196503
García-Martínez J, Aranda A, Pérez-Ortín JE: Genomic run-on evaluates transcription rates for all yeast genes and identifies gene regulatory mechanisms. Molecular Cell 2004,15(2):303-313. 10.1016/j.molcel.2004.06.004
Gardiner CW: Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. Springer, New York, NY, USA; 1983.
Gillespie D: Exact stochastic simulation of coupled chemical reactions. The Journal of Physical Chemistry 1977,81(25):2340-2361. 10.1021/j100540a008
Kauffman S, Peterson C, Samuelsson B, Troein C: Random Boolean network models and the yeast transcriptional network. Proceedings of the National Academy of Sciences of the United States of America 2003,100(25):14796-14799. 10.1073/pnas.2036429100
Kim JT, Martinetz T, Polani D: Bioinformatic principles underlying the information content of transcription factor binding sites. Journal of Theoretical Biology 2003,220(4):529-544. 10.1006/jtbi.2003.3153
Lemon B, Tjian R: Orchestrated response: a symphony of transcription factors for gene control. Genes & Development 2000,14(20):2551-2569. 10.1101/gad.831000
Lewin B: Genes VIII. Prentice-Hall, Upper Saddle River, NJ, USA; 2004.
Lewis D: A qualitative analysis of S-systems: Hopf bifurcation. In Canonical Nonlinear Modeling. S-System Approach to Understanding Complexity. Edited by: Voit E. Van Nostrand Reinhold, New York, NY, USA; 1991:304-344.
Loeve M: Probability Theory, The University Series in Higher Mathematics. Van Nostrand, New York, NY, USA; 1963.
Lorenz EN: Deterministic nonperiodic flow. Journal of the Atmospheric Sciences 1963,20(2):130-141. 10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Lotka AJ: Elements of Physical Biology. Williams and Wilkins, Baltimore, Md, USA; 1925.
Maquat LE: Nonsense-mediated mRNA decay in mammals. Journal of Cell Science 2005,118(9):1773-1776. 10.1242/jcs.01701
McAdams HH, Arkin A: Stochastic mechanisms in gene expression. Proceedings of the National Academy of Sciences of the United States of America 1997,94(3):814-819. 10.1073/pnas.94.3.814
McAdams HH, Arkin A: It's a noisy business! Genetic regulation at the nanomolar scale. Trends in Genetics 1999,15(2):65-69. 10.1016/S0168-9525(98)01659-X
Newman M: The structure and function of complex networks. SIAM Review 2003,45(2):167-256. 10.1137/S003614450342480
Parr RG, Yang W: Density Functional Theory of Atoms and Molecules. Oxford University Press, New York, NY, USA; 1989.
Perko L: Differential Equations and Dynamical Systems. 3rd edition. Springer, New York, NY, USA; 2001.
Peytavi R, Raymond FR, Gagné D, et al.:Microfluidic device for rapid (
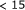 min) automated microarray hybridization. Clinical Chemistry 2005,51(10):1836-1844. 10.1373/clinchem.2005.052845
min) automated microarray hybridization. Clinical Chemistry 2005,51(10):1836-1844. 10.1373/clinchem.2005.052845Ptashne M: Regulated recruitment and cooperativity in the design of biological regulatory systems. Philosophical Transactions of the Royal Society A 2003,361(1807):1223-1234. 10.1098/rsta.2003.1195
Rosenfeld N, Young JW, Alon U, Swain PS, Elowitz MB: Gene regulation at the single-cell level. Science 2005,307(5717):1962-1965. 10.1126/science.1106914
Savageau M, Voit E: Recasting nonlinear differential equations as S-systems: a canonical nonlinear form. Mathematical Biosciences 1987, 87: 83-115. 10.1016/0025-5564(87)90035-6
Sorribas A, Savageau MA: Strategies for representing metabolic pathways within biochemical systems theory: reversible pathways. Mathematical Biosciences 1989,94(2):239-269. 10.1016/0025-5564(89)90066-7
Voit E (Ed): Canonical Nonlinear Modeling. S-System Approach to Understanding Complexity. Van Norstand Reinhold, New York, NY, USA; 1991.
Wang W, Cherry JM, Botstein D, Li H: A systematic approach to reconstructing transcription networks in Saccharomyces cerevisiae. Proceedings of the National Academy of Sciences of the United States of America 2002,99(26):16893-16898. 10.1073/pnas.252638199
Wang R, Jing Z, Chen L: Modelling periodic oscillation in gene regulatory networks by cyclic feedback systems. Bulletin of Mathematical Biology 2005,67(2):339-367. 10.1016/j.bulm.2004.07.005
Wuensche A: Genomic regulation modeled as a network with basins of attraction. Pacific Symposium on Biocomputing (PSB '98), Maui, Hawaii, USA, January 1998 3: 89-102.
Zhang D, Gyorgyi L, Peltier WR: Deterministic chaos in the Belousov-Zhabotinsky reaction: experiments and simulations. Chaos 1993,3(4):723-745. 10.1063/1.165933
Zumdahl S: Chemical Principles. Houghton Mifflin, New York, NY, USA; 2005.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rosenfeld, S. Stochastic Oscillations in Genetic Regulatory Networks: Application to Microarray Experiments. J Bioinform Sys Biology 2006, 59526 (2006). https://doi.org/10.1155/BSB/2006/59526
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/BSB/2006/59526
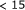 min) automated microarray hybridization. Clinical Chemistry 2005,51(10):1836-1844. 10.1373/clinchem.2005.052845
min) automated microarray hybridization. Clinical Chemistry 2005,51(10):1836-1844. 10.1373/clinchem.2005.052845