- Research Article
- Open access
- Published:
Fixed Points in Discrete Models for Regulatory Genetic Networks
EURASIP Journal on Bioinformatics and Systems Biology volume 2007, Article number: 97356 (2007)
Abstract
It is desirable to have efficient mathematical methods to extract information about regulatory iterations between genes from repeated measurements of gene transcript concentrations. One piece of information is of interest when the dynamics reaches a steady state. In this paper we develop tools that enable the detection of steady states that are modeled by fixed points in discrete finite dynamical systems. We discuss two algebraic models, a univariate model and a multivariate model. We show that these two models are equivalent and that one can be converted to the other by means of a discrete Fourier transform. We give a new, more general definition of a linear finite dynamical system and we give a necessary and sufficient condition for such a system to be a fixed point system, that is, all cycles are of length one. We show how this result for generalized linear systems can be used to determine when certain nonlinear systems (monomial dynamical systems over finite fields) are fixed point systems. We also show how it is possible to determine in polynomial time when an ordinary linear system (defined over a finite field) is a fixed point system. We conclude with a necessary condition for a univariate finite dynamical system to be a fixed point system.
References
Lynch JF: On the threshold of chaos in random Boolean cellular automata. Random Structures & Algorithms 1995, 6(2-3):239-260. 10.1002/rsa.3240060212
Elspas B: The theory of autonomous linear sequential networks. IRE Transactions on Circuit Theory 1959, 6(1):45-60.
Plantin J, Gunnarsson J, Germundsson R: Symbolic algebraic discrete systems theory—applied to a fighter aircraft. Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, La, USA, December 1995 2: 1863-1864.
Bollman D, Orozco E, Moreno O: A parallel solution to reverse engineering genetic networks. In Computational Science and Its Applications—ICCSA 2004—Part 3, Lecture Notes in Computer Science, Springer, Berlin, Germany Edited by: Laganà A, Gavrilova ML, Kumar V et al.. 2004, 3045: 490-497.
Jarrah AS, Vastani H, Duca K, Laubenbacher R: An optimal control problem for in vitro virus competition. Proceedings of the 43rd IEEE Conference on Decision and Control (CDC '), Nassau, Bahamas, December 2004 1: 579-584.
Laubenbacher R, Stigler B: A computational algebra approach to the reverse engineering of gene regulatory networks. Journal of Theoretical Biology 2004, 229(4):523-537. 10.1016/j.jtbi.2004.04.037
Fuller GN, Rhee CH, Hess KR, et al.: Reactivation of insulin-like growth factor binding protein 2 expression in glioblastoma multiforme. Cancer Research 1999, 59(17):4228-4232.
Shmulevich I, Dougherty ER, Zhang W: Gene perturbation and intervention in probabilistic Boolean networks. Bioinformatics 2002, 18(10):1319-1331. 10.1093/bioinformatics/18.10.1319
Hernández Toledo RA: Linear finite dynamical systems. Communications in Algebra 2005, 33(9):2977-2989. 10.1081/AGB-200066211
Bähler J, Svetina S: A logical circuit for the regulation of fission yeast growth modes. Journal of Theoretical Biology 2005, 237(2):210-218. 10.1016/j.jtbi.2005.04.008
Moreno O, Bollman D, Aviño M: Finite dynamical systems, linear automata, and finite fields. Proceedings of the WSEAS International Conference on System Science, Applied Mathematics and Computer Science, and Power Engineering Systems, Copacabana, Rio de Janeiro, Brazil, October 2002 1481-1483.
Sunar B, Cyganski D: Comparison of bit and word level algorithms for evaluating unstructured functions over finite rings. In Proceedings of the 7th International Workshop Cryptographic Hardware and Embedded Systems (CHES '05), Lecture Notes in Computer Science, Edinburgh, UK, August-September 2005 Edited by: Rao JR, Sunar B. 3659: 237-249.
Zivkovic M: A table of primitive binary polynomials. Mathematics of Computation 1994, 62(205):385-386.
Blahut RE: Algebraic Methods for Signal Processing and Communications Coding. Springer, New York, NY, USA; 1991.
Yildirim N, Mackey MC: Feedback regulation in the lactose operon: a mathematical modeling study and comparison with experimental data. Biophysical Journal 2003, 84(5):2841-2851. 10.1016/S0006-3495(03)70013-7
Laubenbacher R: Network Inference, with an application to yeast system biology. Presentation at the Center for Genomics Science, Cuernavaca, Mexico, September 2006 [http://mitla.lcg.unam.mx/]
Laubenbacher R, Stigler B: Mathematical Tools for Systems Biology. http://people.mbi.ohio-state.edu/bstigler/sb-workshop.pdf
Just W: The steady state system problem is NP-hard even for monotone quadratic Boolean dynamical systems. Annals of Combinatorics, in press.
Macdonald BR: Finite Rings with Identity. Marcel Dekker, New York, NY, USA; 1974.
Colón-Reyes O: Monomial dynamical systems, Ph.D. thesis. Virginia Polytechnic Institute and State University, Blacksburg, Va, USA; 2005.
Colón-Reyes O: Monomial Dynamical Systems over Finite Fields. ProQuest, Ann Arbor, Mich, USA; 2005.
Storjohann A:An
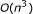 algorithm for the Frobenius normal form. Proceedings of the 23rd International Symposium on Symbolic and Algebraic Computation (ISSAC '98), Rostock, Germany, August 1998 101-104.
algorithm for the Frobenius normal form. Proceedings of the 23rd International Symposium on Symbolic and Algebraic Computation (ISSAC '98), Rostock, Germany, August 1998 101-104.Kaltofen E, Shoup V: Subquadratic-time factoring of polynomials over finite fields. Mathematics of Computation 1998, 67(223):1179-1197. 10.1090/S0025-5718-98-00944-2
Colón-Reyes O, Laubenbacher R, Pareigis B: Boolean monomial dynamical systems. Annals of Combinatorics 2004, 8(4):425-439.
Colón-Reyes O, Jarrah AS, Laubenbacher R, Sturmfels B: Monomial dynamical systems over finite fields. Journal of Complex Systems 2006, 16(4):333-342.
Aho AV, Hopcroft JE, Ullman JD: The Design and Analysis of Computer Algorithms. Addison Wesley, Boston, Mass, USA; 1974.
von zur Gathen J, Gerhard J: Modern Computer Algebra. 2nd edition. Cambridge University Press, Cambridge, UK; 2003.
Ferrer E: A co-design approach to the reverse engineering problem, CISE Ph.D. thesis proposal.
Savas E, Koc CK: Efficient method for composite field arithmetic. Electrical and Computer Engineering, Oregon State University, Corvallis, Ore, USA; 1999.
Ferrer E, Bollman D, Moreno O: Toward a solution of the reverse engineering problem usings FPGAs. In Proceedings of the International Euro-Par Workshops, Lecture Notes in Computer Science, Springer, Dresden, Germany, September 2006 Edited by: Lehner et al.. 4375: 301-309.
Thomas R: Laws for the dynamics of regulatory networks. International Journal of Developmental Biology 1998, 42(3):479-485.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bollman, D., Colón-Reyes, O. & Orozco, E. Fixed Points in Discrete Models for Regulatory Genetic Networks. J Bioinform Sys Biology 2007, 97356 (2007). https://doi.org/10.1155/2007/97356
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/97356
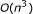 algorithm for the Frobenius normal form. Proceedings of the 23rd International Symposium on Symbolic and Algebraic Computation (ISSAC '98), Rostock, Germany, August 1998 101-104.
algorithm for the Frobenius normal form. Proceedings of the 23rd International Symposium on Symbolic and Algebraic Computation (ISSAC '98), Rostock, Germany, August 1998 101-104.